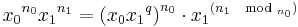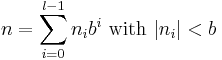Exponentiation by squaring

Exponentiating by squaring is a general method for fast computation of large integer powers of a number. Some variants are commonly referred to as square-and-multiply algorithms or binary exponentiation. In additive notation the appropriate term is double-and-add. These can be of quite general use: for example in modular arithmetic or powering of matrices.

Underlying idea

Using the following observation, one can create a recursive algorithm that computes xⁿ for an integer n using squaring and multiplication:

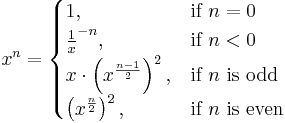
$x^n= \begin{cases} 1, & \mbox{if } n = 0 \\ \frac{1}{x}^{-n}, & \mbox{if } n < 0 \\ x \cdot \left( x^{\frac{n - 1}{2}} \right)^2, & \mbox{if } n \mbox{ is odd} \\ \left( x^{\frac{n}{2}} \right)^2, & \mbox{if } n \mbox{ is even} \end{cases}$

A brief analysis shows that such an algorithm uses log₂n squarings and at most log₂n multiplications. For n > about 4 this is computationally more efficient than naïvely multiplying the base with itself repeatedly.

2^k-ary method

This algorithm calculates the value of xⁿ after expanding the exponent in base 2^k. It was first proposed by Brauer in 1939. In the algorithm below we make use of the following function f(0) = (k,0) and f(m) = (s,u) where m = u·2^s with u odd.

Algorithm:

Input: An element x of G, a parameter k > 0, a non-negative integer n = (n_l−1, n_l−2, ..., n₀)_2^k and the precomputed values x³, x⁵, ..., $x^{2^k-1}$ .

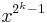Output: The element xⁿ in G

1. y := 1 and i := l-1
2. While i>=0 do
3.    (s,u) := f(n_i)
4.    for j:=1 to k-s do
5.        y := y² 
6.    y := y*x^u
7.    for j:=1 to s do
8.        y := y²
9.    i := i-1
10. return y

For optimal efficiency, k should be the smallest integer satisfying ^[1]

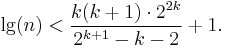
$\lg(n) < \frac{k(k%2B1) \cdot 2^{2k}}{2^{k%2B1} - k - 2} %2B 1.$

Sliding window method

This method is an efficient variant of the 2^k-ary method. For example, to calculate the exponent 398 which has binary expansion (110 001 110)₂, we take a window of length 3 using the 2^k-ary method algorithm we calculate 1,x³,x⁶,x¹²,x²⁴,x⁴⁸,x⁴⁹,x⁹⁸,x⁹⁹,x¹⁹⁸,x¹⁹⁹,x³⁹⁸. But, we can also compute 1,x³,x⁶,x¹²,x²⁴,x⁴⁸,x⁹⁶,x¹⁹²,x¹⁹⁹, x³⁹⁸ which saves one multiplication and amounts to evaluating (110 001 110)n₂

Here is the general algorithm:

Algorithm:

Input: An element 'x' of 'G',a non negative integer n=(n_i,n_i-1,...,n₀)₂, a parameter k>0 and the pre-computed values x³,x⁵,... $x^{2^k-1}$ .

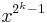Output: The element xⁿ in G

Algorithm:

1.  y := 1 and i := l-1
2.  while i > -1 do
3.      if n_i=0 then y:=y² and i:=i-1
4.      else
5.          s:=max{i-k+1,0}
6.         while n_s=0 do s:=s+1
7.          for h:=1 to i-s+1 do y:=y²
8.          u:=(n_i,n_i-1,....,n_s)₂
9.          y:=y*x^u
10.         i:=s-1
11. return y

Note:

In line 6 the loop finds the longest string of length less than or equal to 'k' which ends in a non zero value. Also not all odd powers of 2 up to 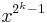$x^{2^k-1}$ need be computed and only those specifically involved in the computation need be considered.

Montgomery's ladder technique

Many algorithms for exponentiation do not provide defence against side-channel attacks. Namely, an attacker observing the sequence of squarings and multiplications can (partially) recover the exponent involved in the computation. This is a problem if the exponent should remain secret, as with many public-key cryptosystems. A technique called Montgomery's Ladder^[2] addresses this concern.

Given the binary expansion of a positive, non-zero integer n=(n_k-1...n₀)₂ with n_k-1=1 we can compute xⁿ as follows:

x₁=x; x₂=x²
for i=k-2 to 0 do
  If n_i=0 then
    x₂=x₁*x₂; x₁=x₁²
  else
    x₁=x₁*x₂; x₂=x₂²
return x₁

The algorithm performs a fixed sequence of operations (up to log n): a multiplication and squaring takes place for each bit in the exponent, regardless of the bit's specific value.

Fixed base exponent

There are several methods which can be employed to calculate xⁿ when the base is fixed and the exponent varies. As one can see, precomputations play a key role in these algorithms.

Yao's method

Yao's method is orthogonal to the 2^k-ary method where the exponent is expanded in radix b=2^k and the computation is as performed in the algorithm above. Let "n", "n_i", "b", and "b_i" be integers.

Let the exponent "n" be written as

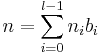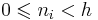$n = \sum_{i=0}^{l-1} n_ib_i$ where $0 \leqslant n_i < h$ for all $i \in [0,l-1]$

Let x_i = x^b_i. Then the algorithm uses the equality

$x^n = \prod_{i=0}^{l-1} {x_i}^{n_i} = \prod_{j=1}^{h-1}{\bigg[\prod_{n_i=j} x_i\bigg]}^j$

Given the element 'x' of G, and the exponent 'n' written in the above form, along with the pre computed values x^b₀....x^b_l-1 the element xⁿ is calculated using the algorithm below

y=1,u=1 and j=h-1
while j > 0 do
for i=0 to l-1 do
1. if n_i=j then u=u*x^b_i
y=y*u
j=j-1
return y

If we set h=2^k and b_i = hⁱ then the n_i 's are simply the digits of n in base h. Yao's method collects in u first those x_i which appear to the highest power h-1; in the next round those with power h-2 are collected in u as well etc. The variable y is multiplied h-1 times with the initial u, h-2 times with the next highest powers etc. The algorithm uses l+h-2 multiplications and l+1 elements must be stored to compute xⁿ (see ^[1]).

Euclidean method

The Euclidean method was first introduced in 'Efficient exponentiation using precomputation and vector addition chains' by P.D Rooij. The algorithm below computes xⁿ using the following equality recursively

${x_0}^{n_0}{x_1}^{n_1}={(x_0{x_1}^{q})}^{n_0} \cdot {x_1}^{(n_1\mod_{n_0})}$

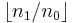
where q= $\lfloor{n_1}/{n_0}\rfloor$

Given the element x in G and the exponent 'n' written as in Yao's method with the pre computed values x^b₀....x^b_l-1 the element xⁿ is calculated using the algorithm below

while true do
Find M such that n_M ≥ n_i for all i in [0,l-1]
Find N ≠ M such that n_N ≥ n_i for all i in [0,l-1], i ≠ M
if n_N ≠ 0 then
q= 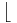$\lfloor$ (n_M/n_N) $\rceil$ , x_N=x_M^q·x_N and n_M=n_N mod n_N
else break
return x_M^n_M

The algorithm first finds the largest value amongst the n_i and then the supremum within the set of {n_i : i ≠ M }. It raises x_M to the power q, multiplies this value with x_N, and then assigns x_N the result of this computation and n_M the value n_M modulo n_N.

Further applications

The same idea allows fast computation of large exponents modulo a number. Especially in cryptography, it is useful to compute powers in a ring of integers modulo q. It can also be used to compute integer powers in a group, using the rule

Power(x, −n) = (Power(x, n))⁻¹.

The method works in every semigroup and is often used to compute powers of matrices,

For example, the evaluation of

13789⁷²²³⁴¹ (mod 2345)

would take a very long time and lots of storage space if the naïve method were used: compute 13789⁷²²³⁴¹ then take the remainder when divided by 2345. Even using a more effective method will take a long time: square 13789, take the remainder when divided by 2345, multiply the result by 13789, and so on. This will take 722340 modular multiplications. The square-and-multiply algorithm is based on the observation that 13789⁷²²³⁴¹ = 13789(13789²)³⁶¹¹⁷⁰. So, if we computed 13789², then the full computation would only take 361170 modular multiplications. This is a gain of a factor of two. But since the new problem is of the same type, we can apply the same observation again, once more approximately halving the size.

The repeated application of this algorithm is equivalent to decomposing the exponent (by a base conversion to binary) into a sequence of squares and products: for example

x¹³ = x^1101_bin

= x^{(1·2^3 + 1·2^2 + 0·2^1 + 1·2^0)}

= x^{1·2^3} · x^{1·2^2} · x^{0·2^1} · x^{1·2^0}

= x^{2^3} · x^{2^2} · 1 · x^{2^0}

= x⁸ · x⁴ · x¹

= (x⁴)² · (x²)² · x

= (x⁴ · x²)² · x

= ((x²)² · x²)² · x

= ((x² · x)²)² · x → algorithm needs only 5 multiplications instead of 12 (13−1)

Some more examples:

x¹⁰ = ((x²)²·x)² because 10 = (1,010)₂ = 2³+2¹, algorithm needs 4 multiplications instead of 9
x¹⁰⁰ = (((((x²·x)²)²)²·x)²)² because 100 = (1,100,100)₂ = 2⁶+2⁵+2², algorithm needs 8 multiplications instead of 99
x^1,000 = ((((((((x²·x)²·x)²·x)²·x)²)²·x)²)²)² because 10³ = (1,111,101,000)₂, algorithm needs 14 multiplications instead of 999
Worked example (with modulo) for the RSA algorithm.

Example implementations

Computation by powers of 2

This is a non-recursive implementation of the above algorithm in Ruby.

In most statically typed languages, result=1 must be replaced with code assigning an identity matrix of the same size as x to result to get a matrix exponentiating algorithm. In Ruby, thanks to coercion, result is automatically upgraded to the appropriate type, so this function works with matrices as well as with integers and floats. Note that n=n1 is redundant when n=n/2 implicitly rounds towards zero, as lower level languages would do. n[0] is the rightmost bit of the binary representation of n, so if it is 1, the number is odd, if it is zero, the number is even.

def power(x,n)
  result = 1
  while n.nonzero?
    if n[0].nonzero?
      result *= x
      n -= 1
    end
    x *= x
    n /= 2
  end
  return result
end

Runtime example: compute 3¹⁰

parameter x =  3
parameter n = 10
result := 1

Iteration 1
  n = 10 -> n is even
  x := x² = 3² = 9
  n := n / 2 = 5

Iteration 2
  n = 5 -> n is odd
      -> result := result * x = 1 * x = 1 * 3² = 9
         n := n - 1 = 4
  x := x² = 9² = 3⁴ = 81
  n := n / 2 = 2

Iteration 3
  n = 2 -> n is even
  x := x² = 81² = 3⁸ = 6561
  n := n / 2 = 1

Iteration 4
  n = 1 -> n is odd
      -> result := result * x = 3² * 3⁸ = 3¹⁰ = 9 * 6561 = 59049
         n := n - 1 = 0

return result

Runtime example: compute 3¹⁰

result := 3
bin := "1010"

Iteration for digit 2:
  result := result² = 3² = 9
  1010_bin - Digit equals "0"

Iteration for digit 3:
  result := result² = (3²)² = 3⁴  = 81
  1010_bin - Digit equals "1" --> result := result*3 = (3²)²*3 = 3⁵  = 243

Iteration for digit 4:
  result := result² = ((3²)²*3)² = 3¹⁰  = 59049
  1010_bin - Digit equals "0"

return result

JavaScript-Demonstration: http://home.mnet-online.de/wzwz.de/temp/ebs/en.htm

Calculation of products of powers

Exponentiation by squaring may also be used to calculate the product of 2 or more powers. If the underlying group or semigroup is commutative then it is often possible to reduce the number of multiplication by computing the product simultaneously.

Example

The formula a⁷×b⁵ may be calculated within 3 steps:

((a)²×a)²×a (four multiplications for calculating a⁷)

((b)²)²×b (three multiplications for calculating b⁵)

(a⁷)×(b⁵) (one multiplication to calculate the product of the two)

so one gets eight multiplications in total.

A faster solution is to calculate both powers simultaneously:

((a×b)²×a)²×a×b

which needs only 6 multiplications in total. Note that a×b is calculated twice, the result could be stored after the first calculation which reduces the count of multiplication to 5.

Example with numbers:

2⁷×3⁵ = ((2×3)²×2)²×2×3 = (6²×2)²×6 = 72²×6 = 31,104

Calculating the powers simultaneously instead of calculating them separately always reduces the count of multiplications if at least two of the exponents are greater than 1.

Using transformation

The example above a⁷×b⁵ may also be calculated with only 5 multiplications if the expression is transformed before calculation:

a⁷×b⁵ = a²×(ab)⁵ with ab := a×b

ab := a×b (one multiplication)

a²×(ab)⁵ = ((ab)²×a)²×ab (four multiplications)

Generalization of transformation shows the following scheme:
For calculating a^A×b^B×...×m^M×n^N
1st: define ab := a×b, abc = ab×c, ...
2nd: calculate the transformed expression a^A−B×ab^B−C×...×abc..m^M−N×abc..mn^N

Transformation before calculation often reduces the count of multiplications but in some cases it also increases the count (see the last one of the examples below), so it may be a good idea to check the count of multiplications before using the transformed expression for calculation.

Examples

For the following expressions the count of multiplications is shown for calculating each power separately, calculating them simultaneously without transformation and calculating them simultaneously after transformation.

Example: a⁷×b⁵×c³
separate: [((a)²×a)²×a] × [((b)²)²×b] × [(c)²×c] ( 11 multiplications )
simultaneous: ((a×b)²×a×c)²×a×b×c ( 8 multiplications )
transformation: a := 2 ab := a×b abc := ab×c ( 2 multiplications )
calculation after that: (a×ab×abc)²×abc ( 4 multiplications ⇒ 6 in total )

Example: a⁵×b⁵×c³
separate: [((a)²)²×a] × [((b)²)²×b] × [(c)²×c] ( 10 multiplications )
simultaneous: ((a×b)²×c)²×a×b×c ( 7 multiplications )
transformation: a := 2 ab := a×b abc := ab×c ( 2 multiplications )
calculation after that: (ab×abc)²×abc ( 3 multiplications ⇒ 5 in total )

Example: a⁷×b⁴×c¹
separate: [((a)²×a)²×a] × [((b)²)²] × [c] ( 8 multiplications )
simultaneous: ((a×b)²×a)²×a×c ( 6 multiplications )
transformation: a := 2 ab := a×b abc := ab×c ( 2 multiplications )
calculation after that: (a×ab)²×a×ab×abc ( 5 multiplications ⇒ 7 in total )

Signed-digit recoding

In certain computations it may be more efficient to allow negative coefficients and hence use the inverse of the base, provided inversion in G is ' fast' or has been precomputed. For example, when computing x^{2^k−1} the binary method requires k−1 multiplications and k−1 squarings . However one could perform k squarings to get x^{2^k} and then multiply by x⁻¹ to obtain x^{2^k−1}.

To this end we define the signed-digit representation of an integer $n$ in radix $b$ as

$n=\sum_{i=0}^{l-1}n_ib^i \text{ with } |n_i|<b$

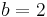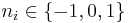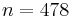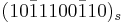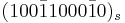'Signed Binary Representation' corresponds to the particular choice $b=2$ and $n_i \in \{-1,0,1\}$ . It is denoted by $(n_{l-1}\dots n_0)_s$ . There are several methods for computing this representation. The representation is not unique, for example take $n=478$ . 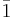Two distinct signed-binary representations are given by $(10\bar 1 1100\bar 1 10)_s$ and $(100\bar 1 1000\bar 1 0)_s$ , where $\bar 1$ is used to denote 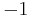$-1$ . Since the binary method computes a multiplication for every non-zero entry in the base 2 representation of $n$ , we are interested in finding the signed-binary representation with the smallest number of non-zero entries, that is, the one with minimal Hamming weight. 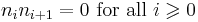One method of doing this is to compute the representation in non-adjacent form, or NAF for short, which is one that satisfies $n_in_{i%2B1}=0\text{ for all }i\geqslant 0$ and denoted by 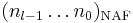$(n_{l-1}\dots n_0)_{\text{NAF}}$ . For example the NAF representation of 478 is equal to 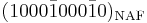$(1000\bar 1 000\bar 1 0)_{\text{NAF}}$ . This representation always has minimal Hamming weight. 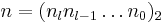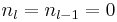A simple algorithm to compute the NAF representation of a given integer $n=(n_ln_{l-1}\dots n_0)_2$ with $n_l=n_{l-1}=0$ is the following:

$c_0=0$
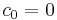
for 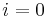$i=0$ to $l-1$ do
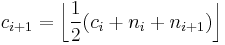
$c_{i%2B1}=\left\lfloor\frac{1}{2}(c_i%2Bn_i%2Bn_{i%2B1})\right\rfloor$
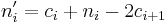
$n_i'=c_i%2Bn_i-2c_{i%2B1}$
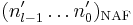
return $(n_{l-1}'\dots n_0')_{\text{NAF}}$

Another algorithm by Koyama and Tsuruoka does not require the condition that 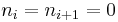$n_i=n_{i%2B1}=0$ ; it still minimizes the Hamming weight.

Alternatives and generalizations

Main article: Addition-chain exponentiation

Exponentiation by squaring can be viewed as a suboptimal addition-chain exponentiation algorithm: it computes the exponent via an addition chain consisting of repeated exponent doublings (squarings) and/or incrementing exponents by one (multiplying by x) only. More generally, if one allows any previously computed exponents to be summed (by multiplying those powers of x), one can sometimes perform the exponentiation using fewer multiplications (but typically using more memory). The smallest power where this occurs is for n=15:

$a^{15} = x \times (x \times [x \times x^2]^2)^2 \!$ (squaring, 6 multiplies)

$a^{15} = x^3 \times ([x^3]^2)^2 \!$ (optimal addition chain, 5 multiplies if x³ is re-used)

In general, finding the optimal addition chain for a given exponent is a hard problem, for which no efficient algorithms are known, so optimal chains are typically only used for small exponents (e.g. in compilers where the chains for small powers have been pre-tabulated). However, there are a number of heuristic algorithms that, while not being optimal, have fewer multiplications than exponentiation by squaring at the cost of additional bookkeeping work and memory usage. Regardless, the number of multiplications never grows more slowly than Θ(log n), so these algorithms only improve asymptotically upon exponentiation by squaring by a constant factor at best.

Notes

^ ^a ^b Cohen, H., Frey, G. (editors): Handbook of elliptic and hyperelliptic curve cryptography. Discrete Math.Appl., Chapman & Hall/CRC (2006)
^ Montgomery, P. L. "Speeding the Pollard and Elliptic Curve Methods of Factorization." Math. Comput. 48, 243-264, 1987.

Exponentiation by squaring

Contents

Underlying idea

2^k-ary method

Sliding window method

Montgomery's ladder technique

Fixed base exponent

Yao's method

Euclidean method

Further applications

Example implementations

Computation by powers of 2

Runtime example: compute 3¹⁰

Runtime example: compute 3¹⁰

Calculation of products of powers

Example

Using transformation

Examples

Signed-digit recoding

Alternatives and generalizations

See also

Notes

Exponentiation by squaring

Contents

Underlying idea

2k-ary method

Sliding window method

Montgomery's ladder technique

Fixed base exponent

Yao's method

Euclidean method

Further applications

Example implementations

Computation by powers of 2

Runtime example: compute 310

Runtime example: compute 310

Calculation of products of powers

Example

Using transformation

Examples

Signed-digit recoding

Alternatives and generalizations

See also

Notes

2^k-ary method

Runtime example: compute 3¹⁰

Runtime example: compute 3¹⁰